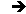En principe, les tables de multiplication sont apprises à l'école primaire et il est très utiles de les maitriser parfaitement avant la fin du collège, car la connaissance des tables de multiplication fait gagner beaucoup de temps ; elle permet :
- d'effectuer de tête beaucoup de calculs simples ;
- d'effectuer les divisions, impossible sinon ;
- de simplifier les fractions et d'effectuer des opérations sur elles ;
- de donner des ordres de grandeur.
NB : Dans ce qui suit, les tables d'addition sont supposées connues, au moins avec une certaine maitrise.
Les astuces présentées dans cet article sont tellement pratiques et assez faciles à mettre en application que l'analyse des tables a été étendue jusqu'à celle de 12. Quelques valeurs utiles ont été ajoutées à la fin : les carrés, quelques cubes, les premiers multiples de 25, les puissances de 2.
→ Voir aussi l'application Apprendre les tables
1. Représentation des tables
Comme pour les tables d'addition, il y a deux façons de représenter les tables de multiplication : une forme complète et une forme compacte.
1.1. Tables chantées
Comme les tables d'addition, celles de multiplications peuvent aussi se chanter : ♫ Na na naa, na ! ♫ Na na naa, na ! ♫ ...
Avec les paroles :
| 1 fois 1 = 1 1 fois 2 = 2 1 fois 3 = 3 1 fois 4 = 4 1 fois 5 = 5 1 fois 6 = 6 1 fois 7 = 7 1 fois 8 = 8 1 fois 9 = 9 1 fois 10 = 10 |
2 fois 1 = 2 2 fois 2 = 4 2 fois 3 = 6 2 fois 4 = 8 2 fois 5 = 10 2 fois 6 = 12 2 fois 7 = 14 2 fois 8 = 16 2 fois 9 = 18 2 fois 10 = 20 |
3 fois 1 = 3 3 fois 2 = 6 3 fois 3 = 9 3 fois 4 = 12 3 fois 5 = 15 3 fois 6 = 18 3 fois 7 = 21 3 fois 8 = 24 3 fois 9 = 27 3 fois 10 = 30 |
4 fois 1 = 4 4 fois 2 = 8 4 fois 3 = 12 4 fois 4 = 16 4 fois 5 = 20 4 fois 6 = 24 4 fois 7 = 28 4 fois 8 = 32 4 fois 9 = 36 4 fois 10 = 40 |
5 fois 1 = 5 5 fois 2 = 10 5 fois 3 = 15 5 fois 4 = 20 5 fois 5 = 25 5 fois 6 = 30 5 fois 7 = 35 5 fois 8 = 40 5 fois 9 = 45 5 fois 10 = 50 |
| 6 fois 1 = 6 6 fois 2 = 12 6 fois 3 = 18 6 fois 4 = 24 6 fois 5 = 30 6 fois 6 = 36 6 fois 7 = 42 6 fois 8 = 48 6 fois 9 = 54 6 fois 10 = 60 |
7 fois 1 = 7 7 fois 2 = 14 7 fois 3 = 21 7 fois 4 = 28 7 fois 5 = 35 7 fois 6 = 42 7 fois 7 = 49 7 fois 8 = 56 7 fois 9 = 63 7 fois 10 = 70 |
8 fois 1 = 8 8 fois 2 = 16 8 fois 3 = 24 8 fois 4 = 32 8 fois 5 = 40 8 fois 6 = 48 8 fois 7 = 56 8 fois 8 = 64 8 fois 9 = 72 8 fois 10 = 80 |
9 fois 1 = 9 9 fois 2 = 18 9 fois 3 = 27 9 fois 4 = 36 9 fois 5 = 45 9 fois 6 = 54 9 fois 7 = 63 9 fois 8 = 72 9 fois 9 = 81 9 fois 10 = 90 |
10 fois 1 = 10 10 fois 2 = 20 10 fois 3 = 30 10 fois 4 = 40 10 fois 5 = 50 10 fois 6 = 60 10 fois 7 = 70 10 fois 8 = 80 10 fois 9 = 90 10 fois 10 = 100 |
Pour certains, ce rabâchage est un bon moyen d'apprendre ces tables. Ce qui est sûr, c'est que cette méthode ne mobilise pas beaucoup l'intelligence des élèves.
1.2. Table de Pythagore
Pythagore était un mathématicien, philosophe et astronome de la Grèce antique, ayant vécu 500 ans avant J.C.
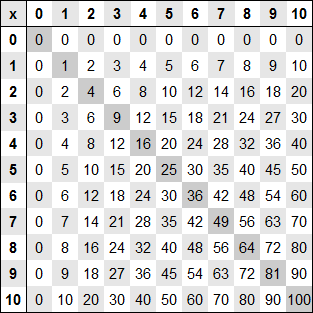
La table de Pythagore est une forme compacte des tables. Le résultat d'une multiplication se trouve à l'intersection de la ligne du premier nombre à multiplier et de la colonne du second.
En supprimant la ligne et la colonne de 0, la ligne et la colonne de 1 affiche les numéros lignes et des colonnes, c'est pourquoi on utilise souvent la forme simplifiée de la table de Pythagore.
La table de Pythagore permet de voir directement certaines propriétés des nombres et de la multiplication. C'est pourquoi la plupart des règles de cet article seront illustrées par leur représentation sur la table de Pythagore.
2. Quelques principes de base
Connaître absolument par cœur ses tables, c'est très bien, mais comprendre comment se combinent les nombres permet de les apprendre bien plus facilement et, quand on ne les sait pas complètement, de deviner une valeur manquante.
Une définition et trois propriétés des nombres entiers vont nous aider : la multiplication à partir de l'addition, la numérotation décimale, la commutativité et la distributivité.
2.1. Multiplication et addition
La multiplication est définie à partir de l'addition.
Exemple : multiplier 3 par 5 revient à additionner 3 fois 5 à lui-même.
3 × 5 = 5 + 5 + 5 = 15
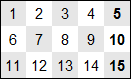Graphiquement, 3 lignes de 5 cases comportent 15 cases.
En superposant les lignes les unes sur les autres, on trouve la surface d'un rectangle de hauteur (ou largeur) 3 et de longueur 5.
Remarquez que le numéro de la dernière case de chaque ligne donne les valeurs de 1 × 5 = 5 ; 2 × 5 = 5 ; 3 × 5 = 15.
Le résultat d'un multiplication par un nombre N s'appelle un multiple de N ou, plus généralement un produit.
Exemple : 15 = 3 × 5 est un multiple de 3 ; comme résultat d'une multiplication, c'est aussi un produit.
2.2. Numérotation décimale
Notre représentation habituelle des nombres est décimale, c'est-à-dire basée sur le nombre de nos doigts : 10.
Exemple : 425 = (4 × 100) + (2 × 10) + 5 : 4 centaines, 2 dizaines et 5 unités.
Cette propriété nous facilitera les multiplications par 10 et par les valeurs qui tournent autour de 10.
2.3. Commutativité
Les deux termes d'une multiplication peuvent être permutés : M × N = N × M
Exemples : 4 × 7 = 7 × 4 = 28 3 × 6 = 6 × 3 = 18. On utilisera donc la forme la plus connue.
En reprenant la définition de la multiplication, on peut basculer un rectangle sans changer sa surface.
Exemple :
3 × 5 = 5 + 5 + 5 = 15
5 × 3 = 3 + 3 + 3 + 3 + 3 = 15
Dans les enchainements de multiplication, cette propriété facilite parfois le calcul mental.
Exemple : 2 × 9 × 5 = (2 × 5) × 9 = 10 × 9 = 90
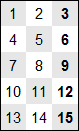
Grâce à elle encore, la table de Pythagore est symétrique par rapport à sa première diagonale. Ainsi, presque la moitié de la table se déduit de l'autre moitié.
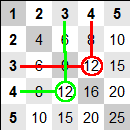Autrement dit, il n'est plus nécessaire d'apprendre les tables chantées que pour les valeurs du second nombre plus petit que le premier, car elles ont déjà été apprises dans une table plus petite. Ex. : dans la table de 4, 4 fois 3 = 12 est déjà dans la table de 3 sous la forme 3 fois 4 = 12 ; il n'est donc utile d'apprendre la table de 4 qu'à partir de 4 fois 4 = 16.
La partie à apprendre de chaque table se réduit donc de plus en plus, au fur et à mesure qu'on en a appris avant. Ici, nous n'aborderons pas les tables dans l'ordre numérique, mais par difficulté croissante. Ainsi, les tables les plus difficile seront réduites à un petit nombre de résultats à apprendre. Sur les illustrations, nous ne laisserons en noir que les valeurs qui restent à apprendre.
2.4. Distributivité
Ce mot savant distributivité signifie qu'un terme de multiplication peut être appliqué sur le second, remplacé par une addition ou une multiplication équivalente. Des exemples seront sans doute plus clairs :
8 × 6 = 8 × (5 + 1) = (8 × 5) + (8 × 1) = 40 + 8 = 48
8 × 6 = 6 × 8 = 8 + 8 + 8 + 8 + 8 + 8 = (8 + 8 + 8 + 8 + 8) + 8 = 40 + 8 = 48
7 × 9 = 7 × (10 – 1) = (7 × 10) – (7 × 1) = 70 – 7 = 63
Il est ainsi possible de déduire une table d'une table voisine déjà connue. En pratique, on ajoutera ou un soustraira 1 à l'un des deux nombres à multiplier, parfois 2 ou plus quand on a plus l'habitude du calcul mental.
C'est aussi grâce à cette propriété que toutes les valeurs d'une colonne C se suivent de C en C ; autrement dit, on passe d'une valeur à celle en-dessous en ajoutant le numéro C de la colonne. Et c'est pareil en passant d'une valeur à celle à sa droite.
3. Table × 0
Le nombre 0 est l'élément absorbant de la multiplication : 0 × N = N × 0 = 0
Multiplier un nombre par 0 le fait disparaitre, le résultat est toujours 0.
Ce résultat est tellement simple que la table × 0 ne figure généralement même pas sur les représentations complètes ou compactes des tables.
4. Table × 1
Le nombre 1 est l'élément neutre de la multiplication : 1 × N = N × 1 = N
Multiplier un nombre par 1 ne le change pas, le résultat est ce nombre.
5. Table × 10
10 × N = N × 10 = N0 : ajouter un 0 après le nombre.
C'est le principe même de la notation décimale des nombres.
Note : La valeur de 10 × N s'appelle le décuple de N.
6. Table × 2
2 × N = N × 2 = N + N: ajouter le nombre à lui-même.
La première moitié de la table de 2 donne la liste des chiffres pairs :
2 × 0 = 0 2 × 1 = 2 2 × 2 = 4 2 × 3 = 6 2 × 4 = 8
Note : La valeur de 2 × N s'appelle le double de N.
7. Table × 5
5 est la moitié de 10, donc 5 × N = N × 5 = (10 × N) / 2 = (N / 2) × 10
Pour les nombres pairs : Diviser N par 2, puis compléter par un 0.
Exemple : 5 × 6 = ? → 6 / 2 = 3 → 5 × 6 = 30
Pour les nombres impairs :
Diviser N par 2 (sans décimale), puis compléter par un 5.
Exemple : 5 × 9 = ? → 9 / 2 = 4... → 5 ×9 = 45
Note : La valeur de 5 × N s'appelle le quintuple de N.
8. Table × 3
Il n'y a pas vraiment d'astuce pour apprendre la table de 3, mais 3 est un petit nombre, donc les multiples de 3 ont des valeurs pas trop grandes, assez faciles à mémoriser. On peut aussi utiliser l'une des deux règles suivantes, la seconde étant un développement de la première :
3 = 2 + 1 = 1 + 1 +1, donc 3 × N = N × 3 = (2 × N) + N = N + N + N : ajouter N à son double, ou ajouter deux fois N à lui-même.
Exemple : 3 × 7 = 7 × 3 = (2 × 7) + 7 = 14 + 7 = 21, ou 3 × 7 = 7 × 3 = 7 + 7 + 7
Note : La valeur de 3 × N s'appelle le triple de N.
9. Table × 9
Il y a plusieurs méthodes pour apprendre la table de 9, toutes basées sur le fait que 9 = 10 – 1.
Première méthode (distributivité) :
9 × N = N × 9 = (10 – 1) × N = (10 × N) – N : ajouter un 0 à N et le soustraire du résultat.
Exemple : 9 × 4 = 4 × 9 = 40 – 4 = 36
Deuxième méthode (complément à 9) :
La somme des chiffres du résultat vaut toujours 9.
Enlever 1 donne la dizaine ; prendre son complément à 9 donne l'unité.
Exemple : 9 × 7 = ? → 7 – 1 = 6 ; 9 – 6 = 3 → 9 × 7 = 63
Troisième méthode (doigt coupé) :
Étaler ses dix doigts devant soi ; replier le N-ième doigt ; le nombre de doigts à gauche donne la dizaine, le nombre de doigts à droite donne l'unité.
Exemple : 9 × 6 = ? → je replie le 6° doigt, il en reste 5 à gauche et 4 à droite → 9 × 6 = 54.
Note : La valeur de 9 × N s'appelle le nonuple de N.
10. Table × 6
La table de 6 se déduit de celle de 5 parce que 6 = 5 + 1, donc 6 × N = N × 6 = (5 + 1) × N = (5 × N) + N
Pour les nombres pairs : Diviser N par 2, puis compléter par N.
Exemple : 6 × 8 = ? → 8 / 2 = 4 → 6 × 8 = 48
Pour les nombres impairs :
Diviser N par 2 (sans décimale), puis compléter par un 5, puis ajouter N.
Exemple : 6 × 7 = ? → 7 / 2 = 3... → 6 × 7 = 35 + 7 = 42
Note : La valeur de 6 × N s'appelle le sextuple de N.
11. Table × 4
4 = 2 × 2, donc 4 × N = N × 4 = (2 × N) × 2 : multiplier par 2, puis multiplier encore par 2.
Exemple: 4 × 8 = (2 × 8) × 2 = 16 × 2 = 32
Note : La valeur de 4 × N s'appelle le quadruple de N.
12. Table × 8
Il n'y a pas de règle simple pour apprendre la table de 8, mais si l'on sait déjà toutes les précédentes, il ne reste plus qu'à mémoriser deux valeurs :
8 × 7 = 7 × 8 = 56 et 8 × 8 = 64
On peut aussi utiliser l'une des deux méthodes suivantes, au moins pour vérifier le résultat si on en est pas sûr :
Première méthode (double du quadruple) :
8 = 4 × 2, donc 8 × N = N × 8 = (4 × N) × 2
Exemple : 8 × 7 = 7 × 8 = (4 × 7) × 2 = 28 × 2 = 56
Deuxième méthode (décuple moins double) :
8 = 10 – 2, donc 8 × N = N × 8 = (10 – 2) × N = (10 × N) – (2 × N) : ajouter un 0 à N et soustraire son double.
Exemple : 8 × 8 = (10 × 8) – (2 × 8) = 80 – 16 = 64
Note : La valeur de 8 × N s'appelle le octuple de N.
13. Table × 7
Il n'y a pas de règle simple pour apprendre la table de 7, mais si l'on sait déjà toutes les précédentes, il ne reste plus qu'à mémoriser une seule valeur :
7 × 7 = 49
Note : La valeur de 7 × N s'appelle le septuple de N.
14. Table des carrés
À partir de la classe de 3°, la connaissance des carrés est utile à la reconnaissance des identités remarquables et à l'application du théorème de Pythagore (encore lui !) dans un triangle.
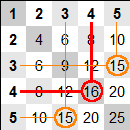N² = N × N : les carrés sont sur la première diagonale de la table de Pythagore.
N² = (N – 1) × (N + 1) + 1 : multiplier le nombre précédent avec le suivant, puis ajouter 1.
Exemple : 4² = (4 – 1) × (4 + 1) + 1 = 3 × 5 + 1 = 15 + 1 = 16
Explication pour ceux qui connaissent l'identité remarquable (a + b) ( a – b) = a² – b² :
avec a = N et b = 1, l'identité devient : (N + 1) (N – 1) = N² – 1. En ajoutant 1, on retrouve N².
Sur la table de Pythagore, un carré est entouré en diagonale par la valeur précédente. Ici, 16 est entre deux 15.
0² = 0 × 0 = 0 1² = 1 × 1 = 1 2² = 2 × 2 = 4 3² = 3 × 3 = 9 4² = 4 × 4 = 16
5² = 5 × 5 = 25 6² = 6 × 6 = 36 7² = 7 × 7 = 49 8² = 8 × 8 = 64 9² = 9 × 9 = 91
10² = 10 × 10 = 100 11² = 11 × 11 = 121 12² = 12 × 12 = 144 15² = 15 × 15 = 225 100² = 100 × 100 = 10 000
15. Tables × 100, × 1000...
100 × N = N00 : ajouter 00 après le nombre ;
1000 × N = N000 : ajouter 000 après le nombre ;
etc.
Exemples : 100 × 7 = 700 ; 1000 × 3 = 3000 ; 10 000 × 4 = 40 000
C'est le principe même de la notation décimale des nombres.
Note : La valeur de 100 × N s'appelle le centuple de N. La valeur de 1000 × N s'appelle le millier de N.
16. Table × 25
25 × 0 = 0 25 × 1 = 25 25 × 2 = 50 25 × 3 = 75 25 × 4 = 100 25 × 5 = 125 etc.
Comme 25 × 4 = 5² × 2² = (5 × 2)² = 10² = 100, tous les multiples de 25 se terminent par 00, 25, 50 ou 75.
On en déduit aussi : 1 / 4 = 0,25 2 / 4 = 1 / 2 = 0,50 = 0,5 3 / 4 = 0,75
Remarquer que 25 = 5² et que 125 = 5³.
17. Table × 11
11 × N = N × 11 = NN : écrire deux fois le chiffre.
Exemple : 8 × 11 = 88
Et aussi : 11 × 11 = 121 11 × 12 = 132
18. Table × 12
12 a beaucoup de diviseurs, il intervient donc dans beaucoup d'exercices et il peut être utile de reconnaitre ses multiples, au moins les premiers :
12 × 2 = 24 12 × 3 = 36 12 × 4 = 48 12 × 5 = 60 12 × 6 = 72
12 × 7 = 84 12 × 8 = 96 12 × 9 = 108 12 × 10 = 120 12 × 11 = 121 12 × 12 = 144
19. Quelques cubes
N³ = N × N × N
0³ = 0 × 0 × 0 = 0 1³ = 1 × 1 × 1 = 1 2³ = 2 × 2 × 2 = 8 3³ = 3 × 3 × 3 = 27
4³ = 4 × 4 × 4 = 64 5³ = 5 × 5 × 5 = 125 10³ = 10 × 10 × 10 = 1000 100³ = 100 × 100 × 100 = 1 000 000
20. Table des puissances de 2
Les puissances de 2 sont la base du système binaire des ordinateurs.
\(2^N = 2\times 2\times \dots \times 2\) : 2 multiplié N fois par lui-même.
\(2^0=1 \quad 2^1=2 \quad 2^2=4 \quad 2^3=8 \quad 2^4=16 \quad 2^5=32 \quad \) \(2^6=64 \quad 2^7=128 \quad 2^8=256 \quad 2^9=512 \quad 2^{10}=1024 \)
21. Pour s'entrainer
Pour ancrer les tables dans sa mémoire, rien ne vaut un peu d'entrainement !
Tu éviteras donc de se précipiter sur ta calculette devant le moindre calcul et tu essaieras plutôt de le résoudre de tête.
On trouve aussi sur l'internet de nombreux sites qui proposent des jeux d'apprentissage. En voici quelques uns :